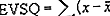Еластична мрежна линеарна регресија користи казне из технике ласо и гребена како би регулисала моделе регресије. Техника комбинује и ласо ЛАССО ЛАССО, скраћено од Оператор најмањег апсолутног скупљања и одабира, статистичка је формула чија је главна сврха одабир и регуларизација карактеристика и методе регресије гребена учењем из њихових недостатака ради побољшања регуларизације статистичких модела.
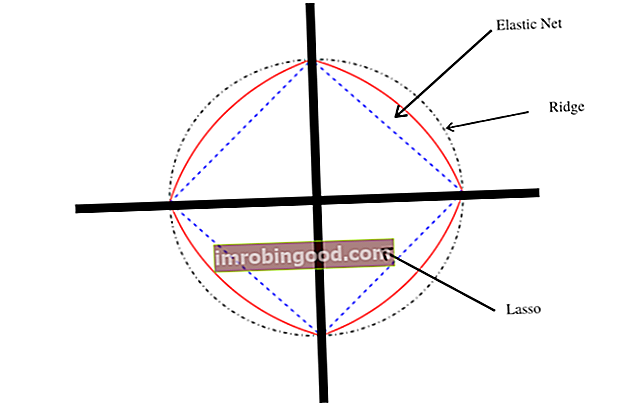
Метода еластичне мреже побољшава ласоова ограничења, тј. Тамо где ласо узима неколико узорака за високодимензионалне податке, поступак еластичне мреже обезбеђује укључивање „н“ броја променљивих до засићења. У случају када су променљиве високо корелиране групе, ласо настоји да изабере једну променљиву из таквих група, а остатак у потпуности игнорише.
Да би се елиминисала ограничења пронађена у ласу, еластична мрежа укључује квадратни израз (|| β || 2) у казну, који када се користи изоловано постаје регресија гребена. Квадратни израз казне изводи функцију губитка ка конвексној. Еластична мрежа се ослања на најбоље из оба света - тј. На регресију ласа и гребена.
У поступку проналажења проценитеља методе еластичне мреже постоје две фазе које укључују и технику ласо и регресије. Прво проналази коефицијенте регресионе гребене, а затим спроводи други корак користећи ласо врсту скупљања коефицијената.
Стога се овом методом коефицијенти подвргавају двема врстама скупљања. Двоструко скупљање од наивне верзије еластичне мреже узрокује ниску ефикасност у предвидљивости и високу пристраност. Да би се исправили такви ефекти, коефицијенти се скалирају множењем са (1 + λ2).
Кратак сажетак
- Метода еластичне мреже истовремено врши избор и регуларизацију променљивих.
- Техника еластичне мреже је најприкладнија тамо где су димензиони подаци већи од броја коришћених узорака.
- Груписање и избор променљивих су кључне улоге технике еластичне мреже.
Еластична геометрија мреже
Када се нанесе на картезијанску раван, еластична мрежа пада између гребена и ласо регресијских плоха, јер је комбинација те две методе регресије. Парцела за еластичну мрежу такође показује сингуларност на врховима, који су важни за проређеност. Такође показује строге конвексне ивице где конвексност зависи од вредности α.
Конвексност је такође зависна од ефекта груписања који зависи од корелације Корелација Корелација је статистичка мера односа две променљиве. Мера се најбоље користи у променљивим које показују линеарни међусобни однос. Уклапање података може се визуелно представити у табели. од изабраних променљивих. Што је већа корелација варијабли, то је већи ефекат груписања, а тиме и већи број променљивих укључених у узорак.
Избор променљивих
Изградња модела захтева избор променљивих да би се формирао подскуп предиктора. Еластична мрежа користи приступ проблема п >> н, што значи да је број бројева предиктора већи од броја узорака који се користе у моделу. Еластична мрежа је прикладна када променљиве формирају групе које садрже високо корелиране независне променљиве Независна променљива Независна променљива је улаз, претпоставка или покретач који се мења како би се проценио њен утицај на зависну променљиву (исход). .
Варијабилни избор је укључен у поступак израде модела како би се помогло у подизању тачности. У случају када је група променљивих у високој корелацији и једна од променљивих је изабрана у узорак, цела група се аутоматски укључује у узорак.
ЦАТРЕГ Инцорпоратион
ЦАТРЕГ је алгоритам који олакшава трансформацију променљивих, линеарних и нелинеарних. Алгоритам користи функције корака и зглоба у трансформисању променљивих било не-монотоно или монотоно у нелинеарним трансформацијама. ЦАТРЕГ може истовремено трансформисати и регулисати променљиве не-монотоно, без нужног потребе да се прво проширују променљиве у основне функције или лажне променљиве.
Еластичне функције нето губитака такође се могу назвати ограниченим типом уобичајене функције регресијског губитка најмањих квадрата. ЦАТРЕГ алгоритам уграђен је у еластичну мрежу, што побољшава ефикасност и једноставност резултујућег алгоритма. У поређењу са тим, еластична мрежа надмашује ласо, који сам надмашује регресију гребена у погледу ефикасности и једноставности.
Регулација еластичне мреже
Током поступка регуларизације, л1 одељак казне чини оскудан модел. С друге стране, квадратни део казне чини л1 део стабилнији на путу ка регуларизацији, елиминише количинско ограничење променљивих које треба изабрати и промовише ефекат груписања.
Ефекат груписања помаже да се променљиве лако идентификују помоћу корелације. То побољшава поступак узорковања. Такође повећава број изабраних променљивих, јер када се једна променљива узоркује у високо корелираној групи, све остале променљиве у тој групи аутоматски се додају у узорак.
Ефективни степени слободе
Ефективни степени слободе мере сложеност модела. Степен слободе важан је током процене или тачног предвиђања уградње модела. Степени слободе су такође укључени у учење линеарних заглађивача. У било којој методи која се односи на л1 казна, нелинеарна природа модела поставља изазов у анализи.
Еластична мрежа се такође може користити у другим применама, на пример у ретком ПЦА, где добија главне компоненте које су модификоване ретким оптерећењима. Друга примена је у еластичној мрежи језгра, где се генерише класа машина језгра са векторима подршке.
Додатна средства
Финанце нуди сертификованог банкарског и кредитног аналитичара (ЦБЦА) ™ ЦБЦА ™ сертификат Цертифиед Банкинг & Цредит Аналист (ЦБЦА) ™ акредитација је глобални стандард за кредитне аналитичаре који покрива финансије, рачуноводство, кредитну анализу, анализу новчаног тока, моделирање уговора, зајмове отплате и још много тога. програм сертификације за оне који желе да своју каријеру подигну на виши ниво. Да бисте наставили да учите и развијате своју базу знања, истражите додатне релевантне финансијске ресурсе у наставку:
- Стабло одлучивања Дрво одлучивања Дрво одлучивања је алат подршке са стаблом сличном структуром који моделира вјероватне исходе, трошкове ресурса, комуналних услуга и могуће посљедице.
- Зависна променљива Зависна променљива Зависна променљива је она која ће се мењати у зависности од вредности друге променљиве, која се назива независна променљива.
- Вишеструка линеарна регресија Вишеструка линеарна регресија Вишеструка линеарна регресија односи се на статистичку технику која се користи за предвиђање исхода зависне променљиве на основу вредности независних променљивих
- Оверфиттинг Оверфиттинг Оверфиттинг је термин који се користи у статистици који се односи на грешку у моделирању која се јавља када функција преуско одговара одређеном скупу података