Временска вредност новца је основни финансијски концепт који држи да новац у садашњости вреди више од исте суме новца која ће се добити у будућности. То је тачно јер новац који имате тренутно можете уложити и зарадити поврат, стварајући тако већи износ новца у будућности. (Такође, код будућег новца постоји додатни ризик да новац из једног или другог разлога заправо никада неће бити примљен.) Временска вредност новца понекад се назива и нето садашња вредност Нето садашња вредност (НПВ) Нето садашња Вредност (НПВ) је вредност свих будућих новчаних токова (позитивних и негативних) током читавог века трајања инвестиције дисконтоване до данас. Анализа НПВ је облик суштинске процене и широко се користи у финансијама и рачуноводству за одређивање вредности посла, инвестиционе сигурности (НПВ) новца.
Како функционише временска вредност новца
Једноставан пример се може користити за приказ временске вредности новца. Претпоставимо да вам неко нуди да вам плати један од два начина за неки посао који радите за њих: Платиће вам сада 1.000 УСД или 1.100 УСД за годину дана.
Коју опцију плаћања бисте требали узети? Зависи од врсте повраћаја инвестиције Стопа поврата Стопа поврата (РОР) је добитак или губитак инвестиције током одређеног временског периода усклађен са почетним трошковима инвестиције израженим у процентима. Овај водич подучава најчешће формуле које тренутно можете зарадити на новцу. Будући да је 1.100 УСД 110% од 1.000 УСД, ако верујете да можете уложити новац у наредних годину дана више од 10%, уложите новац током следеће године, одлучите се да тих 1000 УСД узмете одмах. С друге стране, ако мислите да не бисте могли да зарадите више од 9% у наредних годину дана улагањем новца, требало би да узмете будућу уплату од 1100 УСД - све док верујете да ће вам особа тада платити.
Временска вредност и куповна моћ
Временска вредност новца такође је повезана са концептима инфлације и куповне моћи. Оба фактора треба узети у обзир заједно са било којом стопом поврата која се може остварити улагањем новца.
Зашто је ово битно? Јер инфлација непрестано нагриза вредност, а самим тим и куповну моћ новца. То најбоље илуструју цене роба као што су гас или храна. Ако сте, на пример, 1990. године добили сертификат за 100 долара бесплатног бензина, могли сте да купите много више галона гаса него што бисте могли да сте добили десет долара бесплатног бензина деценију касније.

На инфлацију и куповну моћ морају се рачунати када улажете новац, јер да бисте израчунали свој стварни повраћај улагања, морате одузети стопу инфлације од било ког процента поврата који зарадите на свом новцу. Ако је стопа инфлације у ствари виша од стопе вашег поврата улагања, иако ваша инвестиција показује номинални позитиван принос, ви заправо губите новац у погледу куповне моћи. На пример, ако зарадите 10% од инвестиција, али стопа инфлације износи 15%, заправо сваке године губите 5% куповне моћи (10% - 15% = -5%).
Формула временске вредности новца
Временска вредност новца важан је концепт не само за појединце, већ и за доношење пословних одлука. Предузећа узимају у обзир временску вредност новца при доношењу одлука о улагању у развој нових производа, набавци нове пословне опреме или објеката и успостављању услова кредитирања Уговор о продаји и купопродаји Уговор о купопродаји представља исход кључних комерцијалних преговора и преговора о ценама. У суштини, он износи договорене елементе договора, укључује низ важних заштита свим укљученим странама и пружа правни оквир за довршење продаје имовине. за продају њихових производа или услуга.
За израчунавање вредности може се користити одређена формула будућа вредност новца како би се могао упоредити са садашњом вредношћу:
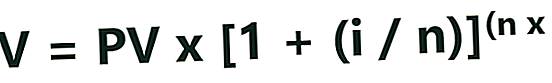
Где:
ФВ = будућа вредност новца
ПВ = садашња вредност
и = каматна стопа или други повраћај који се може зарадити на новцу
т = број година које треба узети у обзир
н = број сложених периода од интереса од године
Користећи горњу формулу, погледајмо пример где имате 5.000 УСД и можете очекивати да ћете сваке године у наредне две године зарађивати камату од 5%. Под претпоставком да се камате састоје само годишње, будућа вредност ваших 5.000 америчких долара данас може се израчунати на следећи начин:
ФВ = 5.000 УСД к (1 + (5% / 1) ^ (1 к 2) = 5.512,50 УСД
Садашња вредност формуле будућег новца
Формула се такође може користити за израчунавање садашња вредност новца који ће се добити у будућности. Једноставно делите будућу вредност уместо да множите садашњу вредност. Ово може бити корисно при разматрању два различита садашња и будућа износа. У нашем оригиналном примеру размотрили смо могућности да неко данас плати ваших 1000 УСД наспрам 1100 УСД годишње. Ако бисте могли зарадити 5% од улагања новца сада и желели бисте да знате која би садашња вредност била једнака будућој вредности од 1100 УСД - или колико новца би вам требало сада на располагању да бисте од сада имали 1100 УСД годишње - формула би бити следећи:
ПВ = 1.100 УСД / (1 + (5% / 1) ^ (1 к 1) = 1.047 УСД
Горњи израчун показује вам да бисте са расположивим приносом од 5% годишње морали да примите 1.047 америчких долара у садашњости да би се изједначили са будућом вредношћу од 1.100 америчких долара које ћете добити годишње за сада.
Да би вам олакшали ствари, постоји низ мрежних калкулатора за израчунавање будуће вредности или садашње вредности новца.
Пример нето садашње вредности
Испод је илустрација како изгледа нето садашња вредност низа новчаних токова. Као што видите, будућа вредност новчаних токова наведена је на врху дијаграма, а садашња вредност новчаних токова приказана је плавим тракама на дну дијаграма.
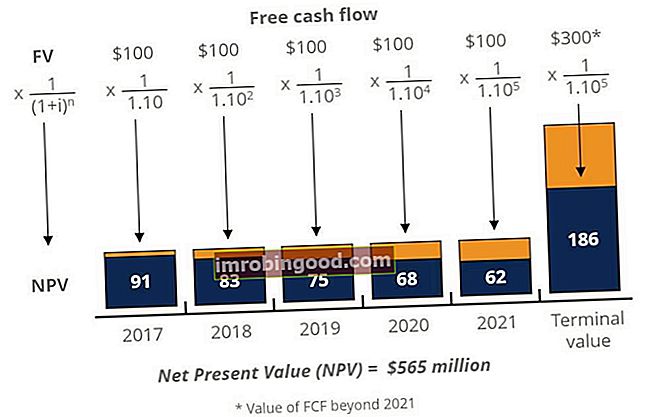
Овај пример је преузет из Финанце’с Фрее Интродуцтион то Цорпорате Финанце Цоурсе, који детаљније покрива ту тему.
Додатна средства
Надамо се да сте уживали у финансијском објашњењу временске вредности новца. Да бисте сазнали више о новцу и улагању, погледајте следеће ресурсе:
- Прилагођена садашња вредност Прилагођена садашња вредност (АПВ) Прилагођена садашња вредност (АПВ) пројекта израчунава се као његова нето садашња вредност плус садашња вредност споредних ефеката финансирања дуга. Погледајте примере и преузмите бесплатни образац. Зашто користити прилагођену садашњу вредност уместо НПВ? Морамо да разумемо како одлуке о финансирању (дуг у односу на капитал) утичу на вредност пројекта
- Методе предвиђања Методе предвиђања Врхунске методе предвиђања. У овом чланку ћемо објаснити четири врсте метода предвиђања прихода које финансијски аналитичари користе за предвиђање будућих прихода.
- НПВ Формула НПВ Формула Водич кроз НПВ формулу у Екцелу приликом обављања финансијске анализе. Важно је тачно разумети како НПВ формула функционише у програму Екцел и математика која стоји иза тога. НПВ = Ф / [(1 + р) ^ н] где је, ПВ = садашња вредност, Ф = будућа уплата (новчани ток), р = дисконтна стопа, н = број периода у будућности
- Методе вредновања Методе вредновања Када се компанија вреднује као временско неограничено пословање, користе се три главне методе процене: ДЦФ анализа, упоредива предузећа и претходне трансакције. Ове методе процене користе се у инвестиционом банкарству, истраживању капитала, приватном капиталу, корпоративном развоју, спајању и преузимању, откупу под леверажом и финансијама