Модел успореног раста је егзогени модел економског раста који анализира промене нивоа производње у привреди током времена као резултат промена у популацији Демографски подаци Демографски подаци се односе на социо-економске карактеристике становништва које предузећа користе за идентификацију преференције производа и понашање купаца у куповини. Са особинама свог циљног тржишта, компаније могу да изграде профил за своју базу купаца. стопа раста, стопа уштеде и стопа технолошког напретка.

Модел Солов Гровтх, који је развио нобеловски економиста Роберт Солов, био је први неокласични модел раста и изграђен је на кејнзијанском Харрод-Домар моделу. Соловов модел је основа савремене теорије економског раста.
Поједностављено представљање модела успореног раста
Испод је поједностављени приказ Солов модела.
Претпоставке:
- Становништво расте константном брзином г. Стога су тренутна популација (представљена са Н) и будућа популација (представљена са Н ’) повезане једначином раста становништва Н’ = Н (1 + г). Ако је тренутно становништво 100, а стопа раста становништва 2%, будуће становништво је 102.
- Сви потрошачи у економији штеде константан део својих прихода и троше остатак. Према томе, потрошња (представљена са Ц) и производња (представљена са И) повезани су једначином потрошње Ц = (1 + с) И. Ако потрошач заради 100 јединица производње као приход, а стопа уштеде износи 40%, тада потрошач потроши 60 јединица, а уштеди 40 јединица.
- Све фирме у економији производе производњу користећи исту производну технологију која узима капитал и рад као инпут. Према томе, ниво производње (представљен И), ниво капитала (представљен К) и ниво рада (представљен Л) повезани су кроз једначину производне функције И = аФ (К, Л).
Модел Солов Гровтх претпоставља да производна функција показује стални повраћај у размере (ЦРС). Под таквом претпоставком, ако удвостручимо ниво залиха капитала и удвостручимо ниво тржишта рада, тржиште рада је место где се понуда и потражња за радним местима сусрећу, а радници или радна снага пружају услуге које послодавци захтевају. Радник може бити свако ко жели да понуди своје услуге за надокнаду, док послодавац може бити један ентитет или организација, ми тачно удвостручујемо ниво производње. Као резултат тога, већи део математичке анализе Солововог модела усредсређен је на излаз по раднику и капитал по раднику уместо на агрегатни оутпут и агрегатни капитал.
- Садашњи капитал (представљен К), будући капитал (представљен К '), стопа амортизације капитала (представљена д) и ниво капиталних инвестиција (представљени И) повезани су једначином акумулације капитала К' = К (1-д) + И.
Решавање модела успореног раста
- У нашој анализи претпостављамо да производна функција има следећи облик: И = аКбЛ1-б где је 0 <б <1. Производна функција је позната као Цобб-Доугласова производна функција, која је најчешће коришћена неокласична производна функција. Заједно са претпоставком да су предузећа конкурентна, тј. Они узимају цену. Такер који узима цену У економији се односи на учесника на тржишту који није у стању да диктира цене на тржишту. Стога, прихватач цена мора прихватити превладавајућу тржишну цену. Преузимачу цена недостаје довољна тржишна снага да утиче на цене добара или услуга. предузећа, коефицијент б је удео капитала (удео прихода који капитал прима).
- Стога се излаз по раднику даје кроз следећу једначину: и = акб где је и = И / Л (излаз по раднику и к = К / Л (капитал по раднику)
- Под претпоставком конкурентске равнотеже добијамо следеће:
- Идентитет прихода и расхода важи као услов равнотеже: И = Ц + И
- Ограничење буџета потрошача: И = Ц + С
- Према томе, у равнотежи: И = С = сИ.
- Једначина акумулације капитала постаје: К ’= (1 – д) К + сИ
- Једначина акумулације капитала у времену по раднику дата је следећом једначином: (1 + г) к '= (1 - д) к + си = (1 - д) к + саф (к) = (1 - д) к + сакб
- Концепт решења који се користи је концепт стабилног стања. Стабилно стање је стање у којем се ниво капитала по раднику не мења. Узмите у обзир графикон испод:
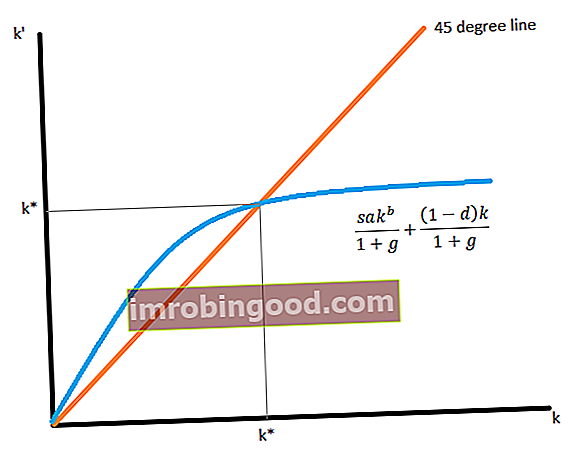
- Стационарно стање се проналази решавањем следеће једначине: к ’= к => (1 + г) к = (1 - д) к + сакб
- Према томе, стабилна вредност капитала по раднику и стабилна вредност производње по раднику су следеће:
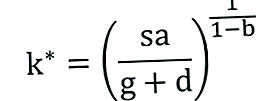
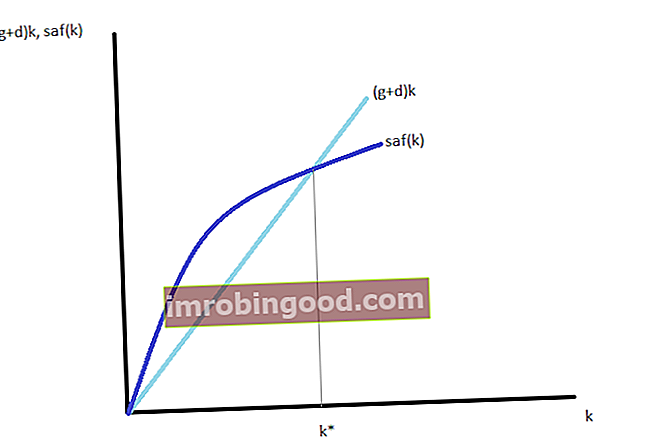
Импликације модела успореног раста
Дугорочно нема раста. Ако земље имају исте г (стопа раста становништва), с (стопа уштеде) и д (стопа амортизације капитала), онда имају исто стабилно стање, па ће се конвергирати, тј. Солов Гровтх Модел предвиђа условну конвергенцију. Тим путем конвергенције сиромашнија земља брже расте.
Земље са различитим стопама штедње имају различита стабилна стања и оне се неће конвергирати, тј. Модел успореног раста не предвиђа апсолутну конвергенцију. Када су стопе штедње различите, раст није увек већи у земљи са нижим почетним капиталом.
Додатна средства
Финанце је званични добављач глобалног аналитичара за финансијско моделирање и вредновање (ФМВА) ™ ФМВА® сертификација Придружите се 350.600+ ученика који раде у компанијама попут Амазона, ЈП Моргана и Ферраријевог сертификационог програма, осмишљеног да помогне свима да постану финансијски аналитичари светске класе . Да бисте наставили напредовати у каријери, корисни ће вам бити додатни финансијски ресурси у наставку:
- Економски показатељи Економски показатељи Економски показатељ је метрика која се користи за процену, мерење и процену укупног здравственог стања макроекономије. Економски показатељи
- Гинијев коефицијент Гинијев коефицијент Гинијев коефицијент (Гинијев индекс или Гинијев однос) статистичко је мерило економске неједнакости у становништву. Коефицијент мери распршеност дохотка или расподелу богатства међу члановима популације.
- Индекс хуманог развоја Индекс хуманог развоја Индекс хуманог развоја (ХДИ) је статистичка мера (сложени индекс) коју су развиле Уједињене нације за процену социјалног и економског развоја земаља широм света. ХДИ узима у обзир три показатеља хуманог развоја, наиме, очекивано трајање живота, образовање и доходак по глави становника.
- Маргинална склоност потрошњи Маргинална склоност потрошњи (МПЦ) односи се на то колико је потрошња у датој економији осетљива на уједињене промене нивоа дохотка. МПЦ као концепт делује слично ценовној еластичности, где се нови увиди могу добити увидом у величину промене потрошње