Прилагођени Р-квадрат је модификована верзија Р-квадрата која узима у обзир предикторе који нису значајни у регресионом моделу. Другим речима, прилагођени Р-квадрат показује да ли додавање додатних предиктора побољшава модел регресије или не. Да бисте разумели прилагођени Р-квадрат, потребно је разумевање Р-квадрата.
Резиме:
- Прилагођени Р-квадрат је модификована верзија Р-квадрата која се прилагођава предикторима који нису значајни у регресионом моделу.
- У поређењу са моделом са додатним улазним променљивим, ниже прилагођени Р-квадрат указује да додатне улазне променљиве не додају вредност моделу.
- У поређењу са моделом са додатним улазним променљивим, виши прилагођени Р-квадрат указује на то да додатне улазне променљиве додају вредност моделу.
Шта је Р-квадрат?
Р-квадрат, који се назива и коефицијент детерминације Коефицијент детерминације Коефицијент детерминације (Р² или р-квадрат) је статистичка мера у регресионом моделу која одређује удео варијансе у зависном, користи се за објашњење степена до које улазне променљиве (предикторске променљиве) објашњавају варијацију излазних променљивих (предвиђене променљиве). Она се креће од 0 до 1. На пример, ако је Р-квадрат 0,9, то указује на то да 90% варијација излазних променљивих објашњава улазне променљиве. Уопштено говорећи, већи Р-квадрат указује на то да боље одговара моделу. Размотрите следећи дијаграм:
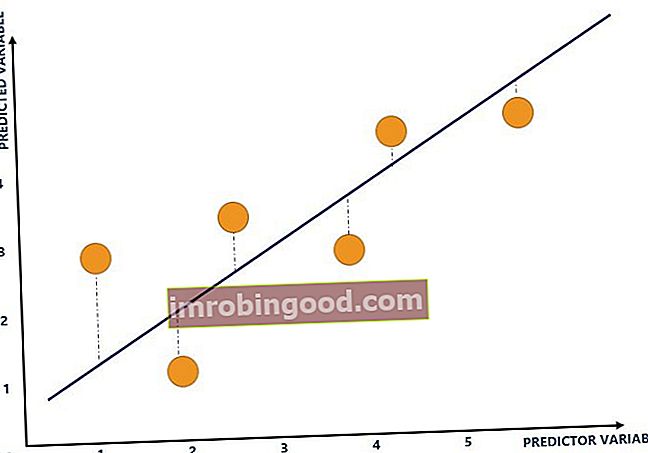
Плава линија односи се на линију која најбоље одговара и показује однос између променљивих. Линија се израчунава путем регресионе анализе. Регресијска анализа. Регресијска анализа је скуп статистичких метода који се користе за процену односа између зависне променљиве и једне или више независних променљивих. Може се користити за процену снаге односа између променљивих и за моделирање будућег односа између њих. и уцртава се тамо где су минимализоване вертикалне удаљености (плаве тачкасте линије) жутих тачака до линије која најбоље одговара.
Жуте тачке односе се на графикон улазних и излазних променљивих. Улазна променљива се црта на к-оси, док се излазна променљива приказује на и-оси. На пример, горњи графикон састоји се од следећег скупа података:

Плаве испрекидане линије односе се на удаљеност графикона улазних и излазних променљивих од линије која најбоље одговара. Р-квадрат изведен је из удаљености свих жутих тачака од линије која најбоље одговара (плава линија). На пример, следећи дијаграм илуструје Р-квадрат 1:

Проблеми са Р-квадратом
Р-квадрат долази са инхерентним проблемом - додатне улазне променљиве учиниће да Р-квадрат остане исти или да се повећа (то је због начина на који се Р-квадрат израчунава математички). Стога, чак и ако додатне улазне променљиве не показују везу са излазним променљивим, Р-квадрат ће се повећати. Пример који објашњава такву појаву наведен је у наставку.
Разумевање прилагођеног Р-квадрата
У основи, прилагођени Р-квадрат гледа да ли додатне улазне променљиве доприносе моделу. Размотрите пример користећи податке које је прикупио власник пице, као што је приказано у наставку:
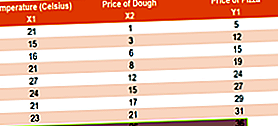
Претпоставимо да власник пице изврши две регресије:
Регресија 1: Цена теста (улазна променљива), Цена пице (излазна променљива)
Регресија 1 даје Р-квадрат од 0,9557 и прилагођени Р-квадрат од 0,9493.
Регресија 2: Температура (улазна променљива 1), Цена теста (улазна променљива 2), Цена пице (излазна променљива)
Регресија 2 даје Р-квадрат 0,9573 и прилагођени Р-квадрат 0,9431.
Иако температура не би смела да има било какву предиктивну моћ на цену пице, Р-квадрат се повећао са 0,9557 (регресија 1) на 0,9573 (регресија 2). Особа може да верује да Регресија 2 носи већу предиктивну моћ пошто је Р-квадрат већи. Иако је улазна променљива температуре бескорисна за предвиђање цене пице, повећала је Р-квадрат. Овде долази прилагођени Р-квадрат.
Прилагођени Р-квадрат гледа да ли додатне улазне променљиве доприносе моделу. Прилагођени Р-квадрат у Регресији 1 био је 0,9493 у поређењу са прилагођеним Р-квадратом у Регресији 2 од 0,9493. Стога је прилагођени Р-квадрат способан да препозна да улазна променљива температуре није од помоћи у објашњавању излазне променљиве (цена пице). У таквом случају, прилагођени Р-квадрат усмерио би творца модела на употребу Регресије 1 уместо Регресије 2.
Пример прилагођеног Р-квадрата
Размотрите два модела:
- Модел 1 користи улазне променљиве Кс1, Кс2 и Кс3 за предвиђање И1.
- Модел 2 користи улазне променљиве Кс1 и Кс2 за предвиђање И1.
Који модел треба користити? Информације у вези са оба модела су дате у наставку:

Упоређујући Р-квадрат између модела 1 и модела 2, Р-квадрат предвиђа да је модел 1 бољи модел јер носи већу моћ објашњења (0,5923 у моделу 1 наспрам 0,5612 у моделу 2).
Упоређујући Р-квадрат између модела 1 и модела 2, прилагођени Р-квадрат предвиђа да улазна променљива Кс3 доприноси објашњавању излазне променљиве И1 (0,4231 у моделу 1 наспрам 0,3512 у моделу 2).
Као такав, треба користити модел 1, јер додатна Кс3 улазна променљива доприноси објашњавању излазне променљиве И1.
Додатна средства
Финанце нуди Финансијско моделирање и вредновање аналитичара (ФМВА) ™ ФМВА® сертификат Придружите се 350.600+ ученика који раде у компанијама попут Амазона, ЈП Моргана и Феррари сертификационог програма за оне који желе да своју каријеру подигну на виши ниво. Да бисте наставили учити и напредовати у каријери, следећи финансијски извори ће вам бити од помоћи:
- Основни појмови о статистици за финансије Основни појмови о статистици о финансијама Чврсто разумевање статистике од пресудне је важности за боље разумевање финансија. Штавише, концепти статистике могу помоћи инвеститорима да надгледају
- Анализа високе и ниске методе наспрам регресионе анализе Високо ниска метода на основу регресионе анализе Високо ниска метода и регресијска анализа су две главне методе процене трошкова које се користе за процену износа фиксних и променљивих трошкова. Менаџери обично морају да поделе мешане трошкове на своје фиксне и променљиве компоненте да би предвидели и планирали будућност.
- Независна променљива Независна променљива Независна променљива је улаз, претпоставка или покретач који се мења да би се проценио њен утицај на зависну променљиву (исход).
- Врсте финансијске анализе Врсте финансијске анализе Финансијска анализа укључује коришћење финансијских података за процену учинка предузећа и давање препорука о томе како се може побољшати у будућности. Финансијски аналитичари свој посао првенствено обављају у програму Екцел, користећи прорачунску табелу за анализу историјских података и израду пројекција Врсте финансијске анализе