ЛАССО, скраћеница од Оператор најмањег скупљања и избора, статистичка је формула чија је главна сврха одабир карактеристика и регуларизација модела података. Методу је први пут представио 1996. године професор статистике Роберт Тибсхирани. ЛАССО уводи параметре у збир модела, дајући му горњу границу која делује као ограничење да збир укључује апсолутне параметре у дозвољеном опсегу.
ЛАССО метода регулише параметре модела смањивањем коефицијената регресије, смањујући неке од њих на нулу. Фаза избора особина се јавља након скупљања, где је изабрана свака различита од нула која ће се користити у моделу. Ова метода је значајна у минимизирању грешака предвиђања које су уобичајене у статистичким моделима Квантитативна анализа Квантитативна анализа је поступак прикупљања и процене мерљивих и проверљивих података као што су приходи, тржишни удео и зараде како би се разумело понашање и учинак посао. У ери технологије података, квантитативна анализа се сматра преферираним приступом доношењу информисаних одлука. .
ЛАССО нуди моделе са високом тачношћу предвиђања. Тачност се повећава с обзиром да метода укључује скупљање коефицијената, што заузврат смањује варијансе и минимализује пристрасност. Најбоље се изводи када је број посматрања низак, а број карактеристика велик. У великој мери се ослања на параметар λ, који је контролни фактор скупљања. Што је већи λ, онда је више коефицијената приморано на нулу.
Када је λ једнако нули, тада модел постаје редовна регресија најмањих квадрата. Сходно томе, када се λ повећава, варијанса се значајно смањује, а пристрасност у резултату такође расте. Ласо је такође корисно средство за уклањање свих променљивих које су ирелевантне и које нису повезане са променљивом одговора.
ЛАССО у статистичким линеарним моделима
Статистички модел је стварни математички приказ проблема. Модел треба да изрази проблем што је могуће ближе стварном свету, а истовремено га чини једноставним и лако разумљивим. Модел се састоји од објашњења и варијабли одговора.
Тхе објашњења променљива је независна променљива о којој дискреционо право има истраживач. Независне променљиве су улазни подаци у моделу које истраживач може мерити како би утврдио њихов ефекат на резултате модела.
Тхе променљива одговора је зависна променљива Зависна променљива Зависна променљива је она која ће се мењати у зависности од вредности друге променљиве, која се назива независна променљива. то чини главни фокус експеримента. Формира резултат експеримента, који може бити појединачни резултат у случају униваријантних модела, или, у случају мултиваријантних модела, више резултата.
ЛАССО чини саставни део процеса израде модела, посебно користећи одабир карактеристика. Фаза избора карактеристика помаже у одабиру објашњавајућих променљивих, које су независне променљиве и, према томе, улазне променљиве у моделу.
Улазне променљиве су важни елементи који одређују излаз модела и који помажу у мерењу њиховог ефекта на променљиве одзива. Избор правих променљивих одређује тачност модела. Фаза избора карактеристика система ЛАССО помаже у правилном одабиру променљивих.
Процена са ЛАССО
Статистички модели се ослањају на ЛАССО за тачан избор променљивих и регуларизацију. У линеарној регресионој регресионој анализи Регресијска анализа је скуп статистичких метода који се користе за процену односа између зависне променљиве и једне или више независних променљивих. Може се користити за процену снаге односа између променљивих и за моделирање будућег односа између њих. , на пример, ЛАССО уводи горњу границу за зброј квадрата, што умањује грешке присутне у моделу. ЛАССО процењивач зависи од параметра λ.
Параметар λ контролише јачину скупљања, при чему повећање λ доводи до повећања скупљања. Горња граница збира свих коефицијената обрнуто је пропорционална параметру λ. Када се горња граница повећа на вредности, параметар λ се смањује. Када се горња граница смањи, параметар λ се истовремено повећава.
Како се горња граница повећава према бесконачности, параметар λ се приближава нули, па претвара експеримент у Обичне најмање квадрате, где је параметар λ увек једнак нули. Када се коефицијенти горње границе приближе нули, вредност параметра λ се повећава према бесконачности.
ЛАССО Геометрија
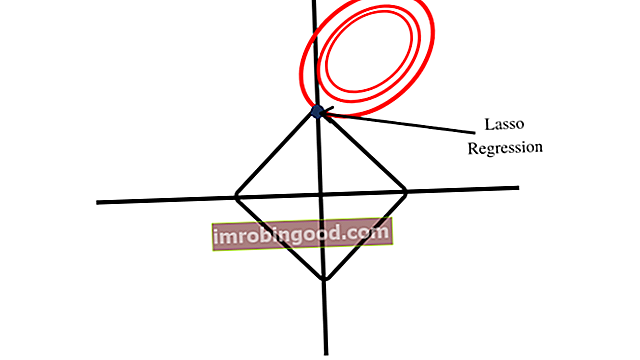
ЛАССО формира дијамантски облик на плочи за своје ограничено подручје, као што је приказано на доњој слици. Дијамантски облик укључује углове, за разлику од кружног облика формираног регресијом гребена. Близина прве тачке до угла показује да модел долази са једним коефицијентом, који је једнак нули.
Област ограничења регресије гребена формира кружни облик који не укључује углове сличне оним који је формиран од подручја ограничења ЛАССО када се црта. Коефицијенти регресионе гребене, према томе, не могу бити једнаки нули.
Пондерисани ЛАССО
Пондерисани ЛАССО резултат је истраживача који изоловано кажњава регресионе коефицијенте. То значи да се уместо кажњавања заједничког параметра λ за све коефицијенте, коефицијенти кажњавају појединачно, користећи различите параметре.
Пондери се могу одредити коришћењем ЛАССО алгоритма за додељивање пондера на одговарајући начин за тачно моделирање. Слично пондерисање коефицијената регресије је и задруга ЛАССО, где се коефицијенти кажњавају у групама које се сматрају сличним.
Додатна средства
Финанце је званични добављач сертификованог банкарског и кредитног аналитичара (ЦБЦА) ™ ЦБЦА ™ сертификација Акредитација сертификованог банкарског и кредитног аналитичара (ЦБЦА) ™ је глобални стандард за кредитне аналитичаре који покрива финансије, рачуноводство, кредитну анализу, анализу новчаног тока, моделирање савеза, отплата зајма и још много тога. програм сертификације, осмишљен да трансформише било кога у финансијског аналитичара светске класе.
Да бисте наставили да учите и развијате своје знање из финансијске анализе, топло препоручујемо додатне финансијске ресурсе у наставку:
- Методе предвиђања Методе предвиђања Врхунске методе предвиђања. У овом чланку ћемо објаснити четири врсте метода предвиђања прихода које финансијски аналитичари користе за предвиђање будућих прихода.
- Независна променљива Независна променљива Независна променљива је улаз, претпоставка или покретач који се мења да би се проценио њен утицај на зависну променљиву (исход).
- Вишеструка линеарна регресија Вишеструка линеарна регресија Вишеструка линеарна регресија односи се на статистичку технику која се користи за предвиђање исхода зависне променљиве на основу вредности независних променљивих
- Анализа сценарија Анализа сценарија Анализа сценарија је техника која се користи за анализу одлука нагађањем различитих могућих исхода у финансијским улагањима. У финансијском моделирању ово

